 |
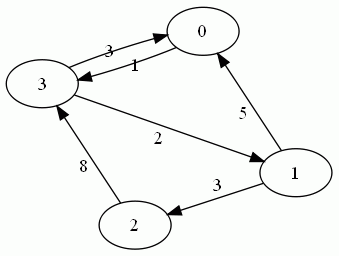
| An example of a directed graph |
Now this problem is all about the edge cases. For example, we need to account for internal loops, as well as for running into dead ends. Now for the purposes of this problem, we're going to assume we're allowed to modify the nodes as we visit them. This is really a matter of convenience, if we could not alter the nodes, we would just have to modify our approach slightly.
At a high level, what we're going to do is build a BFS, utilizing a queue, and keep track of visited nodes by giving them a visited property. We could achieve that effect by keeping a list of visited nodes but it would affect our performance time by requiring us to iterate over it each time we visited a node.
To start, we'll begin at one of the nodes, and traverse the graph until we either find the node we're looking for, or run out of nodes to visit.
Lets look at what the code for this would look like, in javascript:
The algorithm will perform in O(n) time as it must theoretically traverse every node in a worst case scenario, but it has a memory complexity of O(1) as we're not storing anything other than state variables, this changes to O(n^2) and O(n) if we can't modify the nodes as we visit them.
If you wrote an algorithm and would like to test it, here's a super simple graph. 1 and 3 are connected, 3 and 1 are not.
